CSCI 136 - Fall 2019

Data Structures & Advanced Programming

Home | Bill's Lectures | Sam's Lectures | Labs | Handouts & Problem Sets | Links | CS@Williams

Lab 7: The Two Towers (Not a partner lab)

Your goal is to solve a difficult problem using Iterators. (Note: This lab is a variation of the Lab from Chapter 8, modified to use generic classes.)

Pre-lab

Before lab, please do the following: Write an iterator that iterates over the characters of a String. Repeated calls to the iterator’s next() method will return the first character of the string, then the second character, and so on.
More specifically, you are to design and implement a class called CharacterIterator that has the following constructor and method signatures (you may provide additional helper methods and instance variables as you see fit):

          public class CharacterIterator extends AbstractIterator<Character> {
              public CharacterIterator(String str) { ... }
              public Character next() { ... }
              public boolean hasNext() { ... }
              public void reset() { ... }
              public Character get() { ... }
          }
     

The Character class is a wrapper class for primitive char values so that we can use char values with the generic AbstractIterator class. You use Character much like one uses Integer for int values. The Java compiler will automatically convert char values to Character objects as necessary via a technique called “autoboxing.” You may use the following main method to test your code.

            public static void main(String[] args) {
                CharacterIterator ci = new CharacterIterator("Hello world!");
                for (char c : ci) {
                    System.out.println(c);
                }
            }
       

Re-read Chapter 8 in your textbook to review Iterators. I highly recommend you complete your Prelab solution before lab on Wednesday if possible. You will submit it (in a file named CharacterIterator.java) in your git repository at the end of the lab.

Lab Assignment

Goal. To solve a computationally complex problem using iterators. (Note: This lab is a variation of the one given in Chapter 8, modified to use generic classes.)

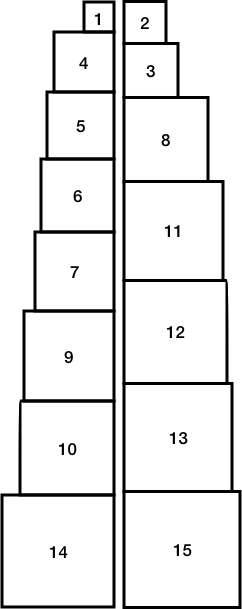
Discussion. Suppose that we are given n uniquely-sized cubic blocks and that each block has a face area between 1 and n. If we build two towers by stacking these blocks, how close can we make their heights? The following two towers, built by stacking 15 blocks, differ in height by only 129 millionths of an inch (each unit is one-tenth of an inch):

Still, this stacking is only the second-best solution! To find the best stacking, we could consider all the possible configurations. We do know one thing: the total height of the two towers is computed by summing the heights of all the blocks. Since the height of each block is the square root of its face area, this is:

If we consider all the subsets of the n blocks, we can think of each subset as representing the set of blocks that make up, say, the left tower. We need only keep track of the subset that comes closest to h/2 without exceeding it (where h is the total height of all n blocks).

In this lab, we will represent a set of n distinct objects with a Vector<Double>, and we will construct an Iterator that returns each of the 2ⁿ subsets.

Understanding the Algorithm

The trick to understanding how to generate a subset of n values from a Vector is to first consider how to generate a subset of indices of elements from 0 to n-1. Once this simpler problem is solved, we can use the indices to help us build a Vector (or subset) of values identified by the indices.

There are exactly 2ⁿ subsets of the values from 0 to n−1. To see this, imagine that you have a strip of paper with n blanks on it, labeled 0 to n−1. Let m be a number 0 ≤ m < n. Choose an arbitrary subset of blocks. If block m is included in a subset, you write a 1 in blank m - 1 on the paper, otherwise you put a 0 in blank m - 1. Since there are 2 * 2 * ... * 2 = 2ⁿ different ways to fill in this strip of paper, there are 2ⁿ different subsets.

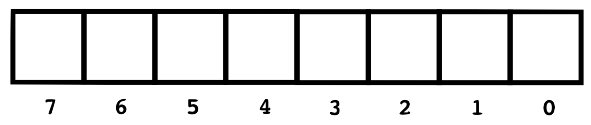
For example, suppose we start with a blank strip of paper.

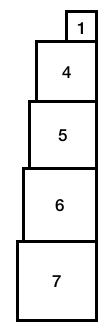
Also suppose that we have eight blocks, labeled 1,2,...,8, and we arbitrarily choose blocks 1, 4, 5, 6, and 7.

So we fill in the appropriate location in the paper for each chosen block (i.e., block m gets a 1 in m - 1).

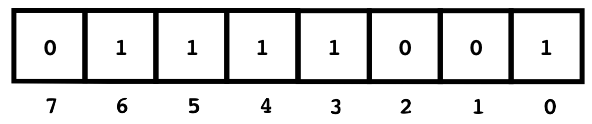
Conveniently, we can think of this strip of paper as determining the digits of an n-bit binary number. For example, the binary number 01111001 is the decimal number 121.

In fact, each number in the range 0 through 2ⁿ−1, when written in binary, uniquely generates a different subset. Given this, we can see a line of attack: just count from 0 to 2ⁿ−1. For each number, use the value of each binary digit (a binary digit is called a bit) to select which blocks are to be included in a subset.

Working with Binary Numbers in Java

Computer scientists work with binary numbers frequently, so there are a number of useful things to remember:

• A Java int type is represented by 32 bits. A Java long is represented by 64 bits. For maximum flexibility, it is useful to use long integers to represent sets of up to 64 elements.
• The arithmetic left shift operator << can be used to quickly compute powers of 2. The value 2ⁱ can be computed by shifting the binary value (1) i places to the left. In Java we write this 1L << i. This trick works only for non-negative, integral powers. The constant 1L is the value one stored as a 64-bit long value. Using this constant ensures that we are using a 64-bit shift operation resulting in a long value instead of a 32-bit operation resulting in an int value. The L is important to ensure that the result is a Long.
• The “bitwise and” of two numbers can be used to determine the value of a single bit in a number’s binary representation. To retrieve bit i of a long integer m, we need only compute m & (1L << i).

Procedure

Armed with this information, the process of generating subsets is fairly straightforward. One approach is the following:

1. Construct a new extension to the AbstractIterator class. This new class should have a constructor that takes a Vector<E> as its sole argument. Subsets of this Vector will be returned as the Iterator progresses. Name this extended class SubsetIterator, and be sure to import structure5.* at the top of your file. Your SubsetIterator should be completely generic. It should know nothing about the values it is iterating over. Thus, the declaration will be:

    public class SubsetIterator<E> extends AbstractIterator<Vector<E>>
   

2. Internally, a long value is used to represent the current subset. This value increases from 0 (the empty set) to 2ⁿ−1 (the entire set of values) as the Iterator progresses.
3. Write a reset method that resets the subset counter to 0.
4. Write a hasNext method that returns true if the current value is a reasonable representation of a subset.
5. Write a get method that returns a new Vector<E> of values that are part of the current subset. If bit i of the current counter is 1, element i of the original Vector is included in the resulting subset Vector.
6. Write a next method. Remember it returns the current subset before incrementing the counter.
7. For an Iterator you would normally have to write a remove method. If you extend the AbstractIterator class, this method is provided and will do nothing (this is reasonable).

Incrementally test. You can now test your SubsetIterator by asking it to print all the subsets of a Vector of values. For example, write a main method for your SubsetIterator class that creates a Vector<Integer> with the first 8 Integers (0 through 7), creates a SubsetIterator<Integer> with this Vector<Integer>, and then prints out all subsets returned. Make sure you end up with all 256 different subsets printed.

Two Towers. To solve the two towers problem, write a main method in a new class called TwoTowers that takes an argument n from the command line. For example,

            $ java TwoTowers 15

should compute the solution of the two towers problem for blocks labeled 1 through 15.

It is easier to proceed by populating your Vector with height values instead of area values. In other words, insert into a Vector<Double> object. To compute the square root of n, you can use the Math.sqrt(n) method. A SubsetIterator is then used to construct 2ⁿ subsets of these values. The values of each subset are summed, and the sum that comes closest to, but does not exceed, the value h/2 is remembered. After all the subsets have been considered, print the best solution. Each block’s height is a square root, so you should print out the area instead.

In addition to printing the best solution, your program should also print the second best solution. In addition to providing an interesting twist to the problem, this has the effect of making it so that you can check the output of your program against the two towers diagram above.

The following is a sample run of the tool:

          $ java TwoTowers 14
          Half height is: 18.298106626967595
          Best subset is: [1, 4, 5, 8, 10, 12, 13] = 18.2964256530161
          Second best subset is: [5, 8, 9, 10, 12, 13] = 18.2964256530161

Thought Questions

In addition, answer the following questions in a file called PROBLEMS.md, and submit it with the rest of your code this week.

1. What is the best solution to the 15-block problem?
2. How long does it take your program to find the answer to the 20-block problem? You may time programs with the Unix time command, as in the following:

    $ time java -Xint TwoTowers 20
   

   (The -Xint flag turns off some optimizations in the Java Virtual Machine and will give you more reliable results.) The output from the time program contains 3 lines:

    real 0m1.588s
    user 0m1.276s
    sys  0m0.922s
   

   If you read the time manual page ($ man 1 time), you can see the meaning of each line. The real line shows the “wall clock” time, which is what we care about. Based on the time taken to solve the 20-block problem, about how long do you expect it would take to solve the 21-block problem? What is the actual time to solve the 21-block problem? How about the 25-block problem (predicted and actual times)? Do these agree with your expectations, given the time complexity of the problem? What about the 40- and 50-block problems? (These will take a very long time. Just estimate based on the runtimes of the smaller problems).
3. This method of exhaustively checking the subsets of blocks will not work for very large problems. Consider, for example, the problem with 50 blocks: there are 2⁵⁰ different subsets. One approach is to repeatedly pick and evaluate random subsets of blocks (stop the computation after 1 second of elapsed time, printing the best subset found). How would you implement randomSubset, a new SubsetIterator method that returns a random subset? (Describe your strategy. You do not need to actually implement it.)

Lab Deliverables

For this lab, please submit the following:

• Your well-documented source code in CharacterIterator.java, SubsetIterator.java, and TwoTowers.java.
• The PROBLEMS.md file that contains answers to the three questions described above, as well as any other information about your submission.

As in all labs, you will be graded on design, documentation, style, and correctness. Be sure to document your program with appropriate comments, including your name and a general description at the top of the file, a description of each method with pre- and post-conditions where appropriate. Also use comments and descriptive variable names to clarify sections of the code which may not be clear to someone trying to understand it.

Submitting Your Lab

As you complete various milestones, you should commit your changes and push them. Commit early and often. When the deadline arrives, we will retrieve the latest version of your code. If you are confident that you are done, please include "Lab Submission" as the commit message for your final commit. If you later decide that you have more edits to make, it is OK. We will look at the latest commit before the deadline.

• Be sure to push your changes to GitHub
• Verify your changes on Github. Navigate in your web browser to your private repository on GitHub. It should be available at https://github.com/williams-cs/cs136f19_lab7_twotowers-{USERNAME} You should see all changes reflected in the various files that you submit. If not, go back and make sure you committed and pushed.

We will know that the files are yours because they are in your git repository. Do not include identifying information in the code that you submit. Our goal is to grade the programs anonymously to avoid any bias. However, in your README.md file, please cite any sources of inspiration or collaboration (e.g., conversations with classmates). We take the honor code very seriously, and so should you. Please include the statement "I am the sole author of the work in this repository" in the comments at the top each of your java files.