Lab 6: Two Towers

This week’s lab explores the use of iterators to help solve difficult computational problems. Be sure that you have read and understood Chapter 8 of Bailey, which introduces the Java Iterator interface.

PRE-LAB: Step 0

Please complete this step by Sunday, 4/12 by 5pm. We will make repositories Sunday night.

Partner preference form: We will assign you a partner for this lab if you would like, but we need some information from you all. We ask that everyone fills out this Google Form by Sunday so we can set up repositories.
- If you know who you would like to partner with, please select your partner’s name.
- If you do not have a specific partner in mind, but you would like us to match you with someone, please select that option and we will pair you.
- If you would like to work alone (we do not recommend this, but understand that collaboration may not be possible in every situation), please select that option.

Note that you can begin working before then! But we need to create your repositories so that you can submit your work and receive feedback.

PRE-LAB: Step 1

To get you started with thinking about the assignment, we would like you to explore iterators with the following warm-up exercise. It is not required that you submit anything for this part of the lab, but we feel that it is well worth the effort to complete this warm-up task.

Warm-up Task

Write an iterator that iterates over the characters of a String. Repeated calls to the iterator’s next() method will return the first character of the string, then the second character, and so on.

More specifically, you should design and implement a class called CharacterIterator that has the following constructor and method signatures (you may provide additional helper methods and instance variables as you see fit):

public class CharacterIterator extends AbstractIterator<Character> {
	public CharacterIterator(String str) { ... }
	public Character next() { ... }
	public boolean hasNext() { ... }
	public void reset() { ... }
	public Character get() { ... }
}

The Character class is a wrapper class for primitive char values so that we can use char values with the generic AbstractIterator class. You use Character much like one uses Integer for int values. The Java compiler will automatically convert char values to Character objects as necessary via a technique called “autoboxing.”

(Don’t forget to import structure5.*.)

You may use the following main method to test your code.

public static void main(String[] args) {
	CharacterIterator ci = new CharacterIterator("Hello world!");
	for (char c : ci) {
		System.out.println(c);
	}
}

When running this program, the output should be the characters of the string "Hello world!", printed one letter per line:

> javac CharacterIterator.java
> java CharacterIterator
H
e
l
l
o

w
o
r
l
d
!

Note that the syntax in the for loop uses the “for thing in things” notation that may be familiar to python programmers. This notation is possible for any iterable structure: since the CharacterIterator extends the AbstractIterator class, and the AbstractIterator class implements Iterable, CharacterIterator implements Iterable.

To get you started, here is a template for the CharacterIterator class.

Lab Assignment

Goal. To solve a computationally complex problem using iterators. (Note: This lab is a variation of the one given in Chapter 8, modified to use generic classes.)

Discussion. Suppose that we are given $n$ uniquely-sized cubic blocks and that each block’s face has an area between $1$ and $n$. If we build two towers by stacking these blocks, how close can we make their heights? The following two towers, built by stacking 15 blocks, differ in height by only 129 millionths of an inch (each unit is one-tenth of an inch):

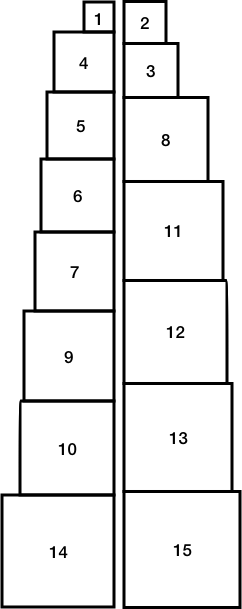
Still, this stacking is only the second-best solution! To find the best stacking, we could consider all the possible configurations. We do know one thing: the total height of the two towers is computed by summing the heights of all the blocks. Since each block’s height is the square root the area of one of it’s faces, the height $h$ is:

$ h = \sum_{i=1}^n \sqrt{i} = \sqrt{1} + \sqrt{2} + ... + \sqrt{n} $

To find the best stacking, we can exhaustively search through every possible combination of the $n$ blocks.

We can think of a “configuration” as representing the set of blocks that make up, say, the left tower (Think about it: given the full set of blocks and the left tower, we can figure out which blocks comprise the right tower…). Our task, then, is to keep track of the configuration that comes closest to $\frac{h}{2}$ without exceeding it (where $h$ is the total height of all $n$ blocks).

In this lab, we will represent a set of $n$ distinct objects with a Vector<Double>, and we will construct an Iterator that returns each of the $2^n$ subsets (configurations of blocks in the left tower).

Understanding the Algorithm

The trick to understanding how to generate a subset of $n$ values from a Vector is to first consider how to generate a subset of indices of elements from $0$ to $n-1$. Once this simpler problem is solved, we can use the indices to help us build a Vector (or subset) of values identified by the indices.

There are exactly $2^n$ subsets of the values from $0$ to $n−1$. To see this, imagine that you have a strip of paper with $n$ blanks on it, labeled $0$ to $n−1$. Let $m$ be a number $0 \leq m < n$. Choose an arbitrary subset of blocks. If block $m$ is included in a subset, you write a 1 in blank $m - 1$ on the paper, otherwise you put a 0 in blank $m - 1$. Since there are $2 \times 2 \times \ldots \times 2 = 2^n$ different ways to fill in this strip of paper, there are $2^n$ different subsets.

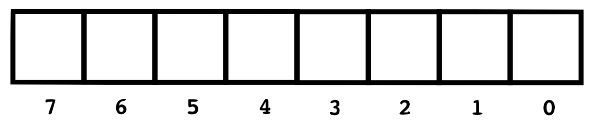
For example, suppose we start with a blank strip of paper.

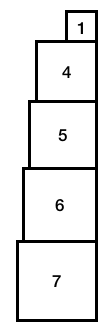
Also suppose that we have eight blocks, labeled $1 \ldots 8$, and we arbitrarily choose blocks $1, 4, 5, 6, $ and $7$.

So we fill in the appropriate location in the paper for each chosen block (i.e., block $m$ gets a 1 in $m - 1$).

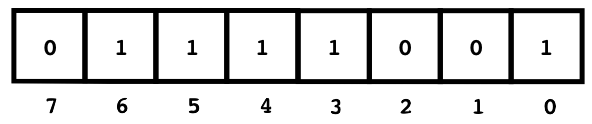
Conveniently, we can think of this strip of paper as determining the digits of an $n$-bit binary number. For example, the binary number 01111001 is the decimal number 121.

In fact, each number in the range $0$ through $2^n−1$, when written in binary, uniquely represents a different subset. Given this observation, we can imagine one solution strategy for exhaustively searching through all possible subsets: just count from $0$ to $2^n−1$. For each number, use the values of the binary digits (a binary digit is called a bit) to select which blocks are to be included in a subset:

If the digit at position $i$ in the number is $1$, include the block at position $i$ in our subset.
If the digit at position $i$ in the number is $0$, omit the block at position $i$ from our subset.

Working With Binary Numbers in Java

Computer scientists work with binary numbers frequently, so there are a number of useful things to remember:

A Java int type is represented by 32 bits. A Java long is represented by 64 bits. For maximum flexibility, it is useful to use long integers so we can represent sets of up to 64 elements.
The arithmetic left shift operator << can be used to quickly compute powers of $2$. The value $2^i$ can be computed by shifting the binary value 1 to the left by $i$ places. In Java we write this as 1L << i. Note that this trick only works for non-negative, integral powers of $2$. The constant 1L is the literal value representing the natural number “one” stored as a 64-bit long value. Using this constant ensures that Java knows we intend to use a 64-bit long value instead of a 32-bit int value. The L is important to ensure that the result is a long!
The “bitwise and” of two numbers can be used to determine the value of a single bit in a number’s binary representation. To retrieve bit $i$ of a long integer m, we need only compute m & (1L << i).

Procedure

Armed with this information, the process of generating subsets is fairly straightforward. One approach is the following:

Construct a new class that extends the AbstractIterator class. This new class should have a constructor that takes a Vector<E> as its sole argument. Subsets of this Vector will be returned as the Iterator progresses. Name this extended class SubsetIterator, and be sure to import structure5.* at the top of your file. Your SubsetIterator should be completely generic. It should know nothing about the values it is iterating over! When we use your SubsetIterator class to solve the particular problem posed in this lab, we will instantiate it to iterate over values of a particular type (Double). But by making SubsetIterator a generic class, we could reuse it to solve other problems that requires us to iterate over subsets of different types of objects. Thus, the class declaration will resemble this:
```
 public class SubsetIterator<E> extends AbstractIterator<Vector<E>> { ... }
```
Internally, a long value should be used to represent the current subset: we will use the representation of this long value’s binary digits to decide which elements are included in the set, and which elements are omitted from the set. This long value should begin at $0$ (all bits are 0, representing the empty set) and increase all the way up to $2^n−1$ ($n$ bits are 1, so all $n$ elements are included in the set) as the Iterator progresses.
Write a reset method that resets the subset counter to $0$.
Write a hasNext method that returns true if the current long value is a reasonable representation of a subset (i.e., it does not specify that you should include elements in the subset that aren’t part of the actual set).
Write a get method that returns a new Vector<E> of values that are part of the current subset. If bit $i$ of the long counter’s current value is $1$, element $i$ of the original Vector is included in the Vector representing the resulting subset.
Write a next method. Remember that next returns the current subset that represented by the state of the counter before incrementing the counter.
For an Iterator, you would normally have to write a remove method. If you extend the AbstractIterator class, this method is provided and will do nothing (this is reasonable for the subset iterator; you do not need to do anything for remove).

Once you have completed your SubsetIterator implementation Incrementally test it! You can test your SubsetIterator by asking it to print all the subsets of a Vector of values. For example, write a main method for your SubsetIterator class that creates a Vector<Integer> with the first $8$ Integers ($0$ through $7$), creates a SubsetIterator<Integer> with this Vector<Integer>, and then prints out all subsets returned. Make sure you end up with all $256$ different subsets printed.

Two Towers. To solve the two towers problem, write a main method in a new class called TwoTowers that takes an argument n from the command line. For example,

$ java TwoTowers 15

should compute the solution of the two towers problem for blocks labeled 1 through 15.

It is easier to proceed by populating your Vector with height values instead of area values. In other words, insert $\sqrt{1}$, $\sqrt{2}$, …, $\sqrt{n}$ into a Vector<Double> object. To compute the square root of $n$, you can use the Math.sqrt(n) method. A SubsetIterator is then used to construct $2^n$ subsets of these values. The values of each subset are summed, and the sum that comes closest to, but does not exceed, the value $\dfrac{h}{2}$ is remembered. After all the subsets have been considered, print the best solution. Each block’s height is a square root, so you should print out the area instead.

In addition to printing the best solution, your program should also print the second best solution. We are adding this requirement for two reasons:

It provides an interesting twist that requires some clever problem-solving (some of the most “obvious” ways of doing this are not correct!)
When you are done, you can now check your solution! Recall, we have provided the second-best stacking for the 15-block problem above.

The following is a sample run of the tool:

$ java TwoTowers 14
Half height (h/2) is: 18.298106626967595
The best subset is: [1, 4, 5, 8, 10, 12, 13] = 18.2964256530161
The second best subset is: [5, 8, 9, 10, 12, 13] = 18.2964256530161

Thought Questions

In addition to completing the lab, please answer the following questions in a file called PROBLEMS.md, and submit it with the rest of your code this week.

What is the best solution to the 15-block problem?
How long does it take your program to find the answer to the 20-block problem? You may time programs with the Unix time command, as in the following:
```
 $ time java -Xint TwoTowers 20
```
(The -Xint flag turns off some optimizations in the Java Virtual Machine and will give you more reliable results.)

The output from the time program contains 3 lines:
```
 real 0m1.588s
 user 0m1.276s
 sys  0m0.922s
```
If you read the time manual page ($ man 1 time), you can see the meaning of each line. The real line shows the “wall clock” time, which is what we care about.

Based on the time taken to solve the 20-block problem, about how long do you expect it would take to solve the 21-block problem? What is the actual time to solve the 21-block problem? How about the 25-block problem (predicted and actual times)? Do these agree with your expectations, given the time complexity of the problem? What about the 40- and 50-block problems? (These will take a very long time. Just estimate based on the runtimes of the smaller problems).
This method of exhaustively checking the subsets of blocks will not work for very large problems. Consider, for example, the problem with 50 blocks: there are $2^{50}$ different subsets. One approach is to repeatedly pick and evaluate random subsets of blocks (stop the computation after 1 second of elapsed time, printing the best subset found). How would you implement randomSubset, a new SubsetIterator method that returns a random subset? (Describe your high-level strategy. You do not need to actually implement it.)

Lab Deliverables

For this lab, please submit the following:

cs136lab07_twotowers-{USERNAMES}/
    README.md
    PROBLEMS.md
    MISTAKES.md
    SubsetIterator.java
    TwoTowers.java

where TwoTowers.java and SubsetIterator.java should contain your well-documented source code.

Recall in previous labs that you had a Java file that contained a convenient main method pre-populated with a variety of helpful tests. It is always a good practice to create a small set of tests to facilitate development, and you are encouraged to do so here.

Submitting Your Lab

We have included a checkbox in your README.md file that you should update when you are done. Delete the x in the box that indicates you are still working on your lab, and mark the x in the box that indicates you are done.

 - [ x ] Not completed, development is still in progress
 - [ ] Completed, this lab is ready for review.

When you push your submission to GitHub, you should see this checkbox clearly updated on your lab’s README.md. This is how we will know that you are done.

Grading

As in all labs, you will be graded on design, documentation, style, and correctness. Be sure to document your program with appropriate comments, a general description at the top of the file, and a description of each method with pre- and post-conditions where appropriate. Also use comments and descriptive variable names to clarify sections of the code which may not be clear to someone trying to understand it.

Whenever you see yourself duplicating functionality, consider moving that code to a helper method. There are several opportunities in this lab to simplify your code by using helper methods.

For the rest of the semester, we will be shifting to a rubric that evaluates labs using a 0-4 scale. Here is the rubric we will be using to evaluate your Two Towers lab submissions:

# Lab Feedback

## Summary Score

| Category       | Score |
| -------------- | ----- |
| Functionality  | . / 4 |
| Design         | . / 4 |
| Documentation  | . / 4 |
| Weighted Score | . / 4 |

---

## Rubric

### Functionality (50%)

Functionality is judged by running your program and inspecting your
code. If you program does not produce the expected results, partial
credit will be assigned based on the specific functionality specified
in the lab assignment.  A well-designed program will comprise several
independent units that can each be tested and verified in
isolation. Writing your programs this way will ensure that we can
award maximum credit for the work that you complete.

Here is a breakdown of the functionality scale:

 0. Lab was not attempted.

 1. Lab is largely incomplete

 2. Most lab infrastructure is present, but key components are largely incorrect.

 3. Functionality is mostly correct or close to correct, but some
    corner cases are missing.

 4. Functionality is correct and complete.

### Design (30%)

Design is judged based on some of the key principles we have discussed
in class and in the readings. Your code should use abstraction in
order to hide/isolate implementation details of classes and your code
should be modular and reusable. This means that the classes that we
write should be self-contained and have their functionality clearly
defined.

Here is a breakdown of the design scale:

 0. Lab was not attempted.

 1. Code is disorganized and does not follow discernible design
    principles.

 2. Code misses many key design principles:

   * Code may use reasonable class structure, but may not wisely allocate
     functionality or define clear abstraction boundaries.

   * Fields and methods may be designated as `public`, `private`, or
     `protected` haphazardly.

   * Functions may be too long or may be unclear.

   * Global variables may be used to communicate across methods,
     rather than performing appropriate parameter passing.

 3. Code largely applies design principles, but may fall short on one
    or more key areas:

   * Logical application of `public`/`private`/`protected` visibility
     modifiers for effective information hiding.

   * Well defined class boundaries.

   * Large tasks are decomposed into concrete subtasks as methods.

   * Little to no unnecessary variables and code.

   * Methods communicate using parameters and return values, rather
     than making assumptions about the state of global variables.

 4. Code is elegant and follows/practices good design principles.

### Documentation (20%)

Documentation is judged on several components:
   * Class-level comments (mandatory)
   * Method-level comments (mandatory)
   * Member variables (documented as needed)
   * In-line comments (describe non-intuitive code as needed)
   * "Overall Quality" of comments/variable naming

Here is a breakdown of the documentation scale:

 0. Code is not documented.

 1. Code is poorly documented:

   * Comments are sparse and/or insufficient to understand the code,
     alternatively, comments may be unhelpful (e.g., comment on *what*
     rather than *why*).

   * Variable/method names are not descriptive.

   * Code is not formatted for readability.

 2. Code documents many methods and classes, but is not thorough:

   * Comments may describe obvious things like `//member variables`,
     rather than details about how the variables should be
     interpreted/used.

   * Comments exist, but are missing components (e.g., pre/post
     conditions for `public` methods)

   * Variable/method names may not always be well-chosen or
     descriptive

 3. Documentation is present and useful:

   * Variable/method names are usually descriptive and follow naming
     conventions.

   * Pre/post conditions are present for `public` methods and and
     assertions are used appropriately.

   * Code is formatted for readability (indentation and whitespace).

   * In-line comments document most non-intuitive code snippets.

 4. Clear, easy-to-read documentation:

   * Code comments follow  [Javadoc](https://www.oracle.com/technetwork/java/javase/documentation/index-137868.html)
     standards.

   * In-line comments document non-intuitive code snippets.

   * All variable/method names are descriptive and follow naming
     conventions.

   * Code is formatted for readability (indentation and whitespace)
     and is therefore easy to read and understand. Logical blocks of
     code are clearly deliniated with whitespace.

   * Pre/post conditions are present for all `public` methods and and
     assertions are used appropriately as documentation and debugging.

The squeaky wheel gets the grease

We are always looking to make our labs better. Please submit answers to the following questions using the anonymous feedback form for this class:

How difficult was this assignment on a scale from 1 to 5 (1 = super easy, …, 5 = super hard)?
Your name (so that I can give you a bonus point).

Bonus: Mistakes

Did you find any mistakes in this writeup? If so, add a file called MISTAKES.md to your GitHub repository and describe the mistakes using bullets. For example, you might write

* Where it says "bypass the auxiliary sensor" you should have written "bypass the primary sensor".
* You spelled "college" wrong ("collej").
* A quadrilateral has four edges, not "too many to count" as you state.

We will try to fix these errors and continue to improve the Labs!