CS134 Lecture 3: Functions

In this notebook there are the following topics/activities:

1. Defining your own funcions
2. Multiple parameters
3. Excercise 1: write your own function average
4. return vs. print
5. Zero-parameter functions
6. Exercise: Computing the Day of the Week
7. Variable Scope

Acknowledgement. This notebook has been adapted adapted from the Wellesley CS111 Spring 2019 course materials (http://cs111.wellesley.edu/spring19).

1. Defining your own functions

Functions are a way of abstracting over computational processes by capturing common patterns.
You have already used built-in functions like print, input and int.
Here is a user-defined function to compute the square of a number.

In [1]:
def square(x):
    """A simple user-defined function."""
    return x * x

Calling or invoking the function: we can call a function many times, but we define it once.

In [2]:
square(5)
Out[2]:
25
In [3]:
square(7)
Out[3]:
49

Parameters

A parameter names "holes" in the body that will be filled in with the argument value for each invocation.

The particular name we use for a parameter is irrelevant, as long as we use the name consistently in the body.

In [6]:
def square(someNumber):
    return someNumber * someNumber

The following function call will generate the same result as the one from the definition of the function with a different parameter name.

In [7]:
square(5)
Out[7]:
25
In [8]:
someNumber

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
<ipython-input-8-2d21d62b5ec2> in <module>
----> 1 someNumber

NameError: name 'someNumber' is not defined

2. Multiple parameters

A function can take as many parameters as needed. They are listed one by one separated by comma.

Important (Order matters!) The order of parameters specifies the order of argument values.

In [9]:
def energy(mass, velocity):
    """Calculate kinetic energy""" 
    return 0.5 * mass * velocity**2

Problem description: A 1 kg brick falls off a high roof. It reaches the ground with a velocity of 8.85 m·s-1. What is the kinetic energy of the brick when it reaches the ground?

Call the function:

In [ ]:
energy(1, 8.85)
In [ ]:
import math
def distanceBetweenPoints(x1, y1, x2, y2):
    """Calculate the distance between points """ 
    return math.sqrt((x2-x1)**2 + (y2-y1)**2)

You are given the following simple graph that depicts two points A and B in the 2-D coordinate system, where every tick is a unit of 1. Call the functioon distanceBetweenPoints with the right values to calculate the distance.

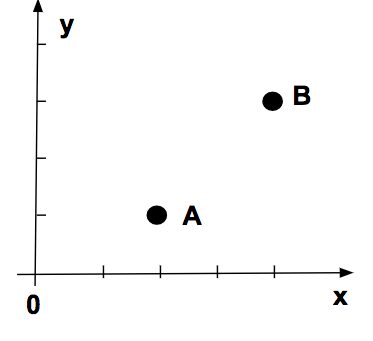
Call the function:

In [ ]:
distanceBetweenPoints(2, 1, 4, 3)

3. Excercise 1: Write your function: average

Define a function named average that takes two numbers and returns the average of the two.

In [10]:
# Here define the function average
def average(num1, num2):
    return (num1+num2)/2

Now try calling your function as below:

In [11]:
average(6,16)
Out[11]:
11.0
In [ ]:

4. return vs. print

  • return specifies the result of the function invocation
  • print causes characters to be displayed in the shell.
In [12]:
def square(x):
    return x*x

def printSquare(a):
    print('Square of', a , 'is', square(a))

Try out the result of the following expressions:

In [13]:
square(3) + square(4)
Out[13]:
25
In [14]:
printSquare(5)

Square of 5 is 25

IMPORTANT: If a function doesn't return a value (but only prints one as a side effect), don't use it in expressions where
a value is expected. Can you guess what result you'll get below:

In [15]:
printSquare(3) + printSquare(4)

Square of 3 is 9
Square of 4 is 16

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
<ipython-input-15-0d212c755bf4> in <module>
----> 1 printSquare(3) + printSquare(4)

TypeError: unsupported operand type(s) for +: 'NoneType' and 'NoneType'

DIGGING DEEPER: See the notes on the None value and the NoneType type to understand in more detail why this happens.

We can verify that None is not a string, by invoking the built-in function type:

In [16]:
type(None)
Out[16]:
NoneType
In [17]:
type(printSquare(3))

Square of 3 is 9
Out[17]:
NoneType
In [20]:
print(print(print(printSquare(3))))

Square of 3 is 9
None
None
None

5. Zero-Parameter Functions

Sometimes it's helpful to define functions that have zero parameters.
Note: you still need parentheses after the function name when defining and invoking the function.

In [21]:
def rocks():
    print("CS134 rocks!")
In [22]:
rocks()
rocks()

CS134 rocks!
CS134 rocks!
In [23]:
# Invoke the same function multiple times
def rocks3():
    rocks()
    rocks()
    rocks()
    
rocks3()

CS134 rocks!
CS134 rocks!
CS134 rocks!

6. Exercise 2: Day of the Week

Suppose we wanted to compute the day of the week for an arbitrary date, specified using a month, day, and year. We'll limit ourselves to dates between 1900 and 2099, inclusive.

The computed remainder tells us the day of the week, where 0 is Saturday.

If you do this in your head, you need to remember a short table of monthly adjustments. Each entry in the table corresponds to a month, where January is month 1 and December is month 12.

Month 1 2 3 4 5 6 7 8 9 10 11 12
Adjusment 1 4 4 0 2 5 0 3 6 1 4 6

Notice that $144$ is $12^2$, $025$ is $5^2$, $036$ is $6^2$, and $146$ is a bit more than $12^2$. If the year is divisible by $4$ (it's a leap year) and the date is January or February, you must subtract 1 from the adjustment.

Now, here's the algorithm:

  1. Write down the date numerically. The date consists of a month between 1 and 12, a day of the month between 1 and 31, and the year in the range 1900-2099.
  1. Compute the monthly adjustment madj.
  1. Compute the number of years year since 1900. Grace Hopper, computer language pioneer, was born December 9, 1906. That would be year 6. Pixel, Iris's dog, was born on May 16, 2018, which is year 118.

  1. Now, compute the sum of the following quantities:

    • the month adjustment madj (eg., 6 for Admiral Hopper)
    • the day of the month
    • the year year
    • the whole number of times 4 divides year (e.g. 1 for Admiral Hopper)

  2. Compute the remainder of the sum of step 4, when divided by 7. The remainder gives the day of the week, where Saturday is 0, Sunday is 1, etc.

Notice that we can compute the remainders before we compute the sum. You may also have to compute the remainder after the sum as well, but if you're doing this in your head, this considerably simplifies the arithmetic.

How might you adjust the algorithm to make the result of 0 indicate Sunday?

John Conway. The above technique is due to John Conway, of Princeton University. Professor Conway answers 10 day of the week problems before gaining access to his computer. His record is well under 15 seconds for 10 correct dates. See Scientist at Work: John H. Conway; At Home in the Elusive World of Mathematics," The New York Times, October 12, 1993.

In [24]:
# Do not worry about how its implemented yet this part yet!
def monthAdjust(month, year):
    '''Function that takes in month in 1-12 and year and returns monthly adjustment'''
    # this is a *list* containing 12 integers.
    adjustments = [1,4,4,0,2,5,0,3,6,1,4,6] 
    # the integers in the adjustment list are indexed 0 through 11
    madj = adjustments[month-1]
    # madj is the adjustment based on the particular month
    if (year%4 == 0) and (month <= 2):  # we will learn if statements in next lecture
        madj -= 1  # shorter way of writing madj = madj - 1
    return madj
In [25]:
monthAdjust(12, 1906)
Out[25]:
6
In [26]:
monthAdjust(2, 2020)
Out[26]:
3
In [27]:
def dayName(dayNum):
    '''Takes day of the week as a number and returns day of 
    the week as a string, where Saturday is 0, Sunday is 1, etc.'''
    # a *list of strings*, indexed between 0 and 6 (remainders, mod 7)
    dayName = ["Saturday", "Sunday", "Monday", "Tuesday", "Wednesday", "Thursday", "Friday"]
    return dayName[dayNum]
In [28]:
dayName(0)
Out[28]:
'Saturday'
In [29]:
dayName(3)
Out[29]:
'Tuesday'
In [30]:
# Let us write out the final function to compute the day of the week.
def dayOfWeek(month, day, year):
    '''This function takes a date as month 1-12, day 1-31, and year (1900-2099)
    as input and returns the day of the week for that date'''
    madj = monthAdjust(month, year)
    year -= 1900 # same as year = year - 1900
    sum = madj + day + year + (year//4)
    rem = sum % 7
    return dayName(rem)
In [31]:
dayOfWeek(2, 12, 2020)  # Today's date
Out[31]:
'Wednesday'
In [32]:
dayOfWeek(8, 15, 1997)  # day of India's independence from British rule
Out[32]:
'Friday'
In [33]:
dayOfWeek(12, 9, 1906)  # Grace Hoppers Birthday!
Out[33]:
'Sunday'

Function calls within a script

So far we have been testing functions interactively and seeing what they return. If we define a function in a python script we must also include a function call that invokes the function.

Main function. To invoke the dayOfWeek function we need the following values from the user: month, day, and year. We can structure these input statements in another function whose purpose it is to get these inputs from the user, call dayOfWeek, and finally print out the solution in a nice user-friendly manner.

In [34]:
# Place your code for gathering user input and calling the dayOfweek function
def main():
    month = int(input("Month (1-12): "))
    day = int(input("Day (1-31): "))
    year = int(input("Year (1900-2099): "))
    # invoke the dayOfWeek function and save return value in a dow variable
    dow = dayOfWeek(month, day, year)
    print('Day of the week for the date ', month, '/', day, '/', year, ' is ', dow, sep = '')
    
# This function call runs the code in main()
main()      

Month (1-12): 2
Day (1-31): 12
Year (1900-2099): 2020
Day of the week for the date 2/12/2020 is Wednesday
In [ ]:

7. Variable Scope

Local variables. An assignment to a variable within a function definition creates/changes a local variable. Local variables exist only within a functions body, and cannot be referred outside of it. Parameters are also local variables that are assigned a value when the function is invoked.

In [ ]:
def square(num):  
    return num*num
In [ ]:
square(5)
In [ ]:
num
In [ ]:
def myfunc (val):
    val = val + 1
    print('local val = ', val)
    return val
In [ ]:
val = 3
newVal = myfunc(val)
In [ ]:
print('global val =', val)
In [ ]:
newVal